Einleitung

Die Spieltheorie ist ein Teilgebiet der Mathematik und Wirtschaftswissenschaften, das sich mit dem strategischen Verhalten von Akteuren in Konfliktsituationen beschäftigt. Spiele werden als mathematische Modelle formuliert, um das rationale Handeln der Spieler und die möglichen Ausgänge zu analysieren.

Ein Nullsummenspiel ist ein Spiel, bei dem der Gewinn eines Spielers dem Verlust des anderen Spielers entspricht. Beispiele für Nullsummenspiele sind Schach, Poker oder Tic-Tac-Toe, bei denen die Spieler entweder gewinnen oder verlieren.

Min-Max Algorithmus

Der Min-Max Algorithmus ist ein Verfahren aus der Spieltheorie und dem maschinellen Lernen, das zur Entscheidungsfindung in Nullsummenspielen eingesetzt wird. Das Ziel des Algorithmus ist es, den optimalen Zug für einen Spieler zu berechnen, indem er die möglichen Züge und deren Konsequenzen analysiert. Der Min-Max Algorithmus basiert auf der Annahme, dass die Spieler rational handeln und versuchen, ihren eigenen Nutzen zu maximieren.

Prinzip

Der Min-Max Algorithmus arbeitet rekursiv und durchsucht den Spielbaum schichtweise. Dabei werden abwechselnd die Züge des Maximierers (Spieler 1) und des Minimierers (Spieler 2) betrachtet. Der Maximierer versucht, den maximalen Nutzen zu erzielen, während der Minimierer versucht, den minimalen Nutzen zu erreichen. Die Nutzenwerte werden dabei entlang des Spielbaums propagiert und am Ende wird der optimale Zug für den Maximierer berechnet.

Beispiel Nim-Spiel Variante

Als Beispiel verwenden wir eine Variante des Nim-Spieles. In dieser Variante starten wir mit einer bestimmten Anzahl an Steichhölzern (z.B. 7). Der erste Spieler teilt diese in zwei Teilgruppen auf, wobei die Anzahl der Streichhölzer nicht gleich sein darf. Der zweite Spieler wählt eine der beiden Teilgruppen und teilt sie erneut in zwei Teilgruppen auf. Das Spiel endet, wenn keine neue Teilgruppe mehr gebildet werden kann.

Die erste Gruppe mit 7 Streichhölzer kann also in eine der folgende Teilgruppen aufgeteilt werden

• 1 und 6
• 2 und 5
• 3 und 4

Wählt der erste Spieler zum Beispiel die Aufteilung in die Teilgruppen 2 und 5, so hat der zweite Spieler nun folgende Möglichkeiten:

• Die 5 werden aufgeteilt in 1 und 4, damit ergibt sich die Aufteilung 1, 2 und 4
• Die 5 werden aufgeteilt in 2 und 3, damit ergibt sich die Aufteilung 2, 2 und 3
• Die 2 können nicht aufgeteilt werden, da die Teilgruppen die gleiche Anzahl hätten

Baumdarstellung

Die möglichen Züge und deren Konsequenzen können in einem Spielbaum dargestellt werden. Jeder Knoten im Baum repräsentiert einen Spielzustand, der durch die Anzahl der Streichhölzer und den Spieler bestimmt wird. Die Kanten des Baumes stellen die möglichen Züge dar, die zu einem neuen Spielzustand führen.

Die folgende Abbildung zeigt den Spielbaum für das Nim-Spiel mit 7 Streichhölzern: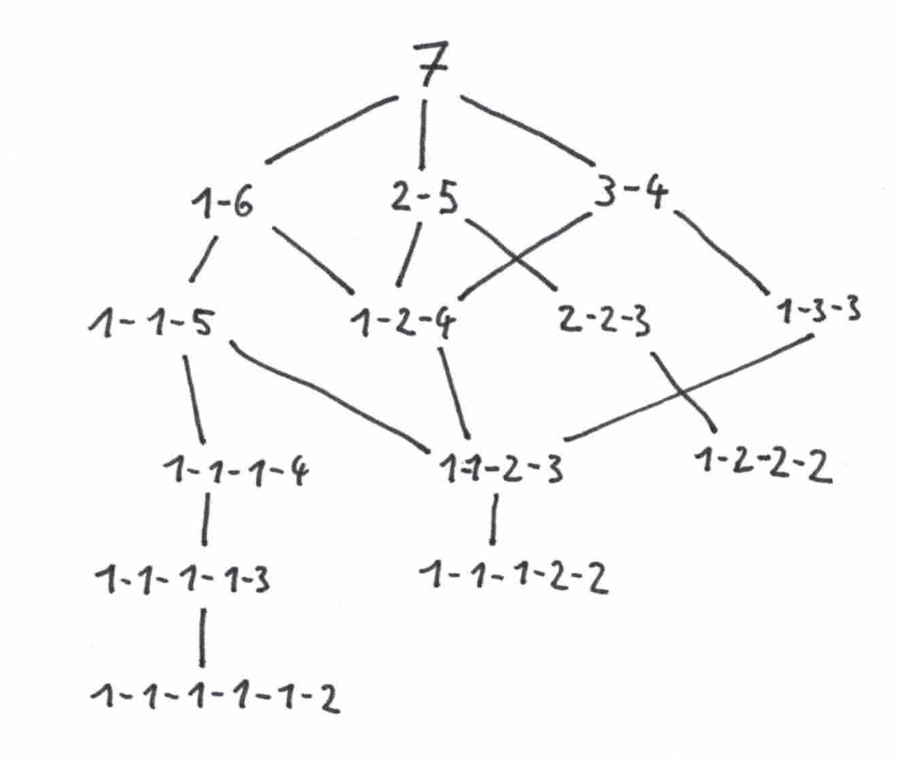

Min-Max Anwendung

• Wir starten mit der Zuordnung der Spieler. Hier startet unser Gegenspieler "They".
• Ist gibt drei Endzustände in diesem Spiel:
  • 1-1-1-1-1-2: Diesen Zug hat unser Gegenspieler gemacht und wir verlieren. Es wird mit -1 markiert
  • 1-1-1-2-2: Diesen Zug haben wir gemacht und dadurch gewinnen wir. Es wird mit +1 markiert
  • 1-2-2-2: Diesen Zug hat wieder unser Gegenspieler gemacht und wir verlieren. Es wird mit -1 markiert

Nun werden die einzelnen Knoten bewertet. Unser Gegenspieler wird den Knoten wählen, der zu einem Minimum führt, wir wählen den Knoten der zu einem Maximum führt.

Vollständiger gelöster Baum: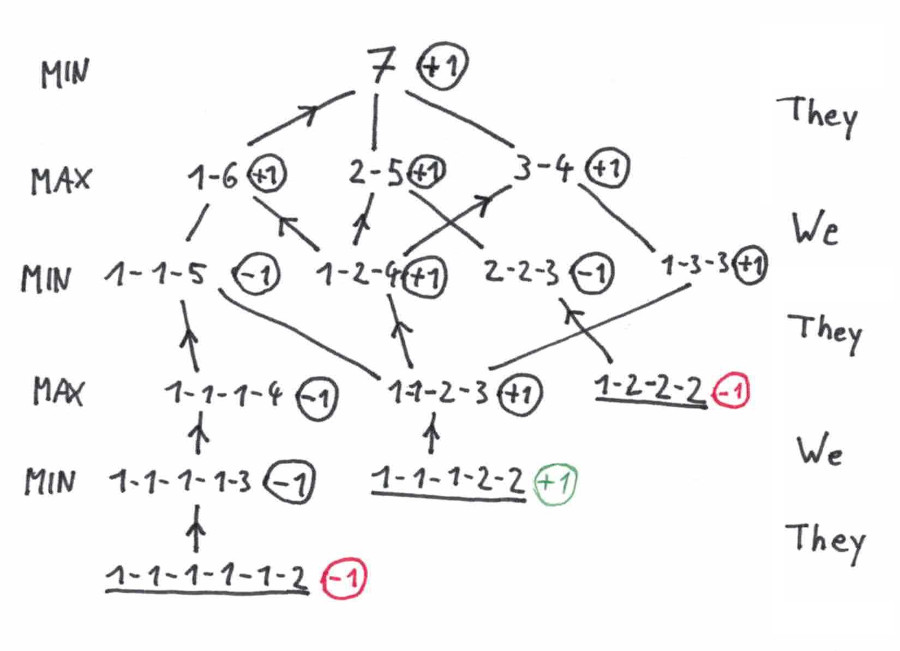

Wir sehen, dass unser Gegenspieler keine Chance auf einen Sieg hat, sofern wir keinen Fehler machen.